Latent Semantic Anal...
潜语义分析(LSA,Latent Semantic Analysis; 有时也称作,LSI, Latent Semantic Indexing)是文本建模和分析中常用的模型。LSA是Deerwester, Dumais等在1990年提出的,它引入了矩阵计算中的奇异值分解(SVD, Singular Value Decomposition)和低秩矩阵近似(Low Rank Approximation),对文档集的表示矩阵进行分析,将文档映射到潜语义空间,达到文档潜语义表示和降维的目的。
1.文档的表示
文档表示是文本分析中的基本问题,它可以将人可读文档转化为机器可读数据结构。常用的文本表示方法有向量空间模型(VSM, Vector Space Model),它是一种简单且有效的文档表示方法,广泛的应用于信息检索系统中。
向量空间模型将文档表示为向量,向量的每个维度代表词表中的一个词,对应的值代表的是该词在文档中出现的(加权)次数。
向量空间模型可以很方便的计算出文档与文档之间,文档与查询(query)之间的相似度,度量一般采用cosine相似度(cosine非严格的距离度量方式,其不满足距离度量的三个要素—非负、对称、三角不等式)。
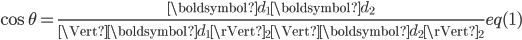
其中,
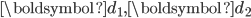 是文档的空间向量模型表示,
是文档的空间向量模型表示, 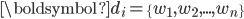 ,
, 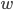 为词
为词 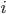 的权重(可以是Boolean值,也可以是TF-IDF等值),
的权重(可以是Boolean值,也可以是TF-IDF等值), 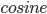 相似度在
相似度在 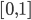 之间。
之间。VSM模型简单,计算方便,可以方便的计算出文档的相关系数(
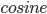 等),但是VSM模型认为单词之间是独立的,只是简单的表示了文档,并没有引入语法,上下文环境或者语义信息;向量维度为词表大小,当词表较大时,向量会很稀疏;在文档匹配时,长文档的相似度值会过小。
等),但是VSM模型认为单词之间是独立的,只是简单的表示了文档,并没有引入语法,上下文环境或者语义信息;向量维度为词表大小,当词表较大时,向量会很稀疏;在文档匹配时,长文档的相似度值会过小。2.SVD
奇异值分解是将矩阵分解成三个特定矩阵——正交矩阵
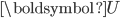 ,对角矩阵
,对角矩阵 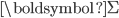 ,正交矩阵的转置
,正交矩阵的转置 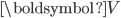 :
: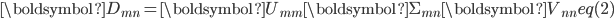
其中,
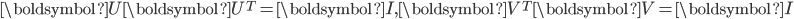 ,
, 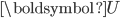 中的列向量是矩阵
中的列向量是矩阵 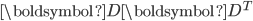 的正交特征向量,
的正交特征向量, 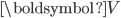 中的列向量是矩阵
中的列向量是矩阵 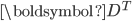 ,
, 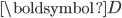 的正交特征向量,
的正交特征向量, 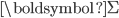 中对角元素为特征值的平方根降序排列
中对角元素为特征值的平方根降序排列 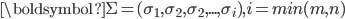 。
。3.Low Rank Approximation
低秩矩阵近似是一个最小化问题,它是在满足近似矩阵的秩的约束下,代价函数(cost function)最小,它的代价函数是原始矩阵(数据矩阵)和近似矩阵之间的差值。

其中,
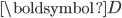 表示原始矩阵(数据矩阵),
表示原始矩阵(数据矩阵), 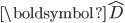 表示近似矩阵,
表示近似矩阵, 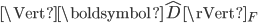 表示矩阵D的Frobenius范数。
表示矩阵D的Frobenius范数。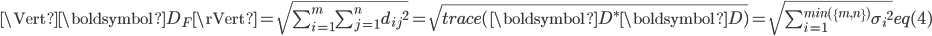
其中,
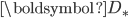 是
是 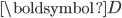 的共轭转置,当
的共轭转置,当 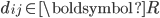 时,
时, 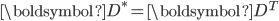 。低秩矩阵近似可以通过奇异值分解来得到解
。低秩矩阵近似可以通过奇异值分解来得到解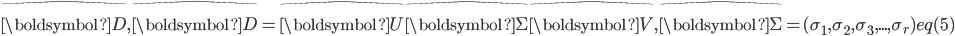
4.LSA
前文提到LSA是引入了SVD和低秩矩阵近似进行文本分析。在LSA中,模型通过对文档集表示矩阵(文档-词矩阵)进行奇异值分解,并低秩矩阵近似对文档集表示矩阵进行近似,得到K维空间中的文档-潜语义、潜语义-词的表示矩阵。
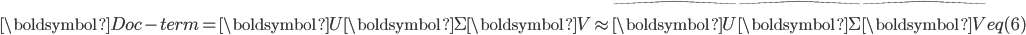
其中,
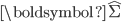 为对角方阵,
为对角方阵, 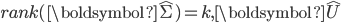 为文档-潜语义表示矩阵,
为文档-潜语义表示矩阵, 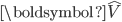 为潜语义-词表示矩阵。
为潜语义-词表示矩阵。 图1
图15.Extension
LSI局限于
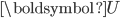 和
和 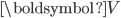 正交性假设,SVD的计算时间为
正交性假设,SVD的计算时间为 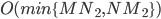 ,其中
,其中 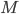 为文档集表示矩阵的行数,
为文档集表示矩阵的行数, 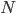 为数据矩阵的列数。LSI在处理超大规模文档时,很难高效的求解,模型的可扩展性低。在对文档集表示矩阵进行SVD时,得到的表示无法保证稀疏化,这样得到的结果(文档topic表示)会很稠密。
为数据矩阵的列数。LSI在处理超大规模文档时,很难高效的求解,模型的可扩展性低。在对文档集表示矩阵进行SVD时,得到的表示无法保证稀疏化,这样得到的结果(文档topic表示)会很稠密。 图2
图25.1 RLSI(Regularized LSI)
在LSI的基础上,RLSI[Wang etc., 2013]对文档的主题表示和主题-词之间关系上加入稀疏化控制,同时去除LSI中
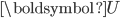 和
和 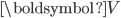 正交性假设。按照训练环境,RLSI分为batch-RLSI和online-RLSI,Batch-LSI其定义如下:
正交性假设。按照训练环境,RLSI分为batch-RLSI和online-RLSI,Batch-LSI其定义如下:
其中,
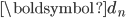 表示第n篇文档的表示向量,
表示第n篇文档的表示向量, 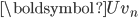 是对
是对 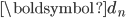 近似表示,
近似表示, 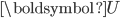 为主题-词的表示矩阵,
为主题-词的表示矩阵, 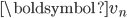 为第n篇文档的主题表示向量,
为第n篇文档的主题表示向量, 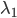 控制
控制 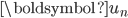 的稀疏程度,当
的稀疏程度,当 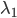 越大,
越大, 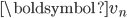 越稀疏;
越稀疏; 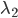 控制
控制 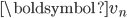 的收缩(Shrinkage)程度,当
的收缩(Shrinkage)程度,当 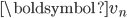 越大,
越大, 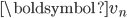 的收缩程度越大。
的收缩程度越大。 图-3
图-3上式对于
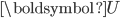 和
和 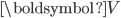 为非凸问题,但是对于单一的
为非凸问题,但是对于单一的 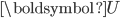 或
或 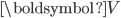 ,为凸问题。如此,求解上式只需要给定一个变量(
,为凸问题。如此,求解上式只需要给定一个变量( 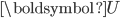 或
或 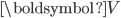 ),求解另一变量。
),求解另一变量。 图-4
图-4(1)给定
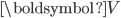 ,更新
,更新 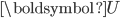
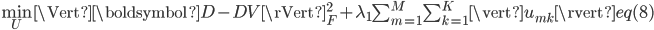
令
 ,如此,式(7)可以表示为:
,如此,式(7)可以表示为: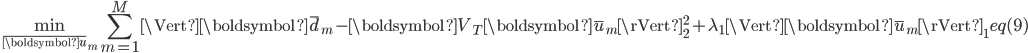
式(8)可以分解成M个独立的优化问题,每个问题形式为:
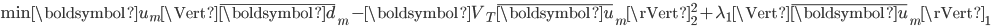
式(9)是一个
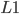 -正则的最小二乘问题,求解方法有多种,比如内点法(Interior Point Method),软阈值的坐标下降(Coordination Descent with Soft-thresholding),Lars-Lasso方法等。以软阈值梯度下降法为例,每次迭代过程中,选取
-正则的最小二乘问题,求解方法有多种,比如内点法(Interior Point Method),软阈值的坐标下降(Coordination Descent with Soft-thresholding),Lars-Lasso方法等。以软阈值梯度下降法为例,每次迭代过程中,选取 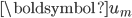 的一个元素
的一个元素 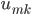 ,固定剩余的元素,求解式(9)。将式(9)包含
,固定剩余的元素,求解式(9)。将式(9)包含 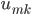 的项单独列出,记为
的项单独列出,记为 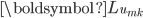 。
。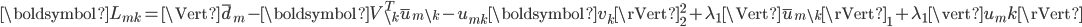

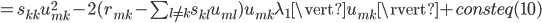
其中,
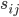 和
和 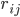 为对应矩阵
为对应矩阵 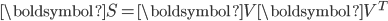 和
和 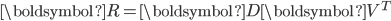 。上式对应的解为如下形式:
。上式对应的解为如下形式: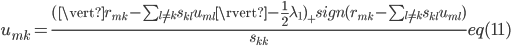
其中,
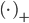
 图-5
图-5(2)给定
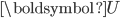 ,更新
,更新 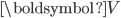
类似问题(1),更新
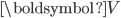 的过程也可以分解成
的过程也可以分解成 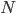 个独立的优化问题。
个独立的优化问题。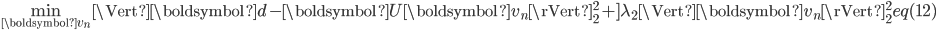
式(12)为
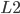 -正则的最小二乘问题(统计上,称为岭回归(Ridge Regression)),解为:
-正则的最小二乘问题(统计上,称为岭回归(Ridge Regression)),解为: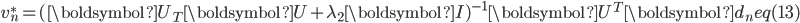
 图-6
图-65.2 Online-RLSI
在处理流式文档数据时,文档是按序一一到达,且文档中包含的主题是不断变化的。Online-RLSI可以有效的跟踪话题演化(Topic tracking)。类似式(6),目标方程为:

式(14)中第一项是
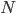 个文档的“经验损失(Empirical Loss)”,第二项控制模型复杂度(L1-正则)。
个文档的“经验损失(Empirical Loss)”,第二项控制模型复杂度(L1-正则)。在online-RLSI中,文档是相互独立的。当文档
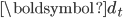 到达时,online-RLSI将文档投射到主题空间,然后更新主题-词矩阵。
到达时,online-RLSI将文档投射到主题空间,然后更新主题-词矩阵。Online-RLSI通过式(15)得到文档
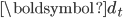 在主题空间的投射,
在主题空间的投射,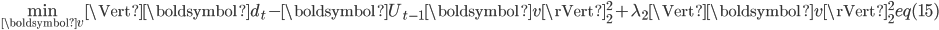
其中,
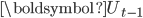 为上次迭代得到的主题-词矩阵。
为上次迭代得到的主题-词矩阵。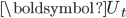 可以通过求解如下问题得到,
可以通过求解如下问题得到,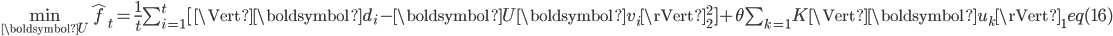
类比于batch-RLSI,式(15)是式(12)的近似,式(16)是式(14)的近似。
(1)文档投影
文档投影问题是一个L2正则的最小二乘问题,其解为
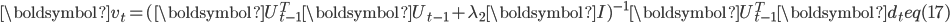
(2)更新主题-词矩阵
式(16)等同于下式,
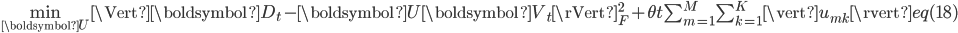
其中,
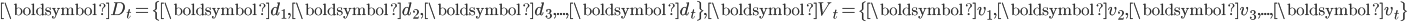 。类似于式(7)的求解,可以将式(18)分解为
。类似于式(7)的求解,可以将式(18)分解为 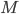 个子问题,
个子问题,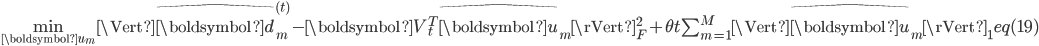
令
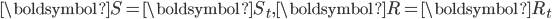 ,式(19)的解可以通过图2中所示算法求解。在online-RLSI中,
,式(19)的解可以通过图2中所示算法求解。在online-RLSI中, 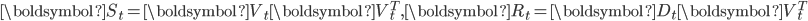 。
。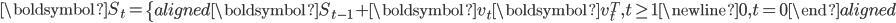
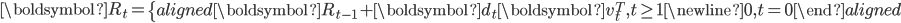
 图-7
图-76.Conclusion
LSI模型(扩展模型)相对后续介绍的pLSA,LDA,DP等比较简单,仅用常用矩阵分解方式对文档-词矩阵进行分析,同时LSI模型没有对应的概率生成过程描述,无法用概率图模型表示。
7.参考文献
[1].Dumais, S. T. (2004). Latent semantic analysis. Annual review of information science and technology, 38(1), 188-230.
[2].Wikipedia. Latent Semantic Analysis, http://en.wikipedia.org/wiki/Latent_s
emantic_indexing.
[3].Lee, D. D., & Seung, H. S. (2001). Algorithms for non-negative matrix factorization. In Advances in neural information processing systems (pp. 556-562).
[4].Hoyer, P. O. (2004). Non-negative matrix factorization with sparseness constraints. The Journal of Machine Learning Research, 5, 1457-1469.
[5].Strang, G. (2003). Introduction to linear algebra. Cambridge Publication.
[6].Wikipedia. Non-negative Matrix Factorization. http://en.wikipedia.org/wiki/Non-negative_matrix_factorization
[7].Wikipedia. Singular Value Decomposition. http://en.wikipedia.org/wiki/Singular_
value_decomposition
[8].Quan Wang, Jun Xu, Hang Li, and Nick Craswell. (2013). Regularized Latent Semantic Indexing: A New Approach to Large-Scale Topic Modeling. ACM Trans. Inf. Syst. 31
留下你的评论