The Advanced Matrix ...

我爱计算机 5年前 发在 人工智能, 博客, 数学, 机器学习 0

本文转载自：https://sites.google.com/site/igorcarron2/matrixfactorizations ，列举很有用的矩阵分解的资料，居家旅行必备之良药啊。

The Advanced Matrix Factorization Jungle

Welcome to The Advanced Matrix Factorization Jungle


[ A living document on the state of the art matrix factorization algorithms and their numerous implementations ]
 
 
Table of Content
  • Introduction
    • Why this page ?
    • Contributions
    • Heuristics and Phase transitions
    • Notations
  • Randomized Algorithms  ( Randomized Numerical Linear Algebra (RandNLA))
  • Kernel Factorizations
  • Spectral Clustering, A = DX  with unknown D and X, solve for sparse X and X_i = 0 or 1 
  • K-Means / K-Median: A = DX  with unknown D and X, solve for XX^T = I and X_i = 0 or 1
  • Subspace Clustering, A = AX  with unknown X, solve for sparse/other conditions on X  
  • Graph Matching: A = XBX^T with unknown X, B solve for B and X as a permutation
  • NMF: A = DX with unknown D and X, solve for elements of D,X positive
  • Generalized Matrix Factorization, 

    W.*L − W.*UV′ with W a known mask, U,V unknowns solve for U,V and L lowest rank possible
  • Matrix Completion, A = H.*L with H a known mask, L unknown solve for L lowest rank possible
  • Stable Principle Component Pursuit (SPCP)/ Noisy Robust PCA,  A = L + S + N with L, S, N unknown, solve for L low rank, S sparse, N noise
  • Robust PCA : A = L + S with L, S unknown, solve for L low rank, S sparse
  • Sparse PCA: A = DX  with unknown D and X, solve for sparse D 
  • Dictionary Learning: A = DX  with unknown D and X, solve for sparse X 
  • Archetypal Analysis: A = DX with unknown D and X, solve for D = AB with  D, B positive
  • Matrix Compressive Sensing (MCS), find a rank-r matrix L such that A(L) ~= b / or A(L+S) = b
  • Multiple Measurement Vector (MMV) Y = A X with unknown X and rows of X are sparse.
    • Compressive Sensing, Y = A X with unknown X and rows of X are sparse, X is one column.
  • Blind Source Separation (BSS) Y = A X with unknown A and X and statistical independence between columns of X or subspaces of columns of X
  • Partial and Online SVD/PCA
  • Other factorizations
    • D(T(.)) = L + E with unknown L, E and unknown transformation T and  solve for transformation T, Low Rank L and Noise E
    • Boolean Matrix Factorization
  • Tensor Decomposition
  • Frameworks featuring advanced Matrix factorizations
From [1]


 
Introduction
 
Why this page ?
 
Matrix Decompositions has a long history and generally centers around a set of known factorizations such as LU, QR, SVD and eigendecompositions. More recent factorizations have seen the light of the day with constraints on the factors as in NMF, k-means and related algorithms [1]. However, with the advent of new methods based on random projections and convex optimization that started in part in the compressive sensing literature, we are seeing a surge of very diverse algorithms implementations dedicated to many different kinds of matrix factorizations with new constraints based on rank and/or positivity and/or sparsity, et,... As a result of these developmenets, this page aims at keeping a list of downloadable implementations here following the success of the big picture in compressive sensing.
 
Contributions
The sources for this list include the following most excellent sites: 
who provide more in-depth additional information.  Additional implementations are featured on Nuit Blanche. The following people provided additional inputs to this page:
Your name can be listed here too if you provide relevant context/links to this document. 
 
Heuristics and Phase transitions
 
For each factorization identified in this document, I have added an item called Phase Transition that features papers, websites that have explored the set of parameters for which the heuristics of the implementation of these factorizations work or not. It turns out that in many cases these phase transitions are sharp. In compressive sensing, we call it the Donoho-Tanner phase transition for L_1 type of solvers. If you have found or written about a phase transition for any of these factorizations, please kindly let me know about it.
 
In particular, most of the algorithms listed below rely on using the heuristics of the nuclear norm as a proxy to the rank functional. It may not be optimal. Currently, CVX ( Michael Grant and Stephen  Boyd) consistently allows one to explore other proxies than the rank functional such as the log-det as found by Maryam  Fazell, Haitham Hindi, Stephen Boyd and others. One could argue that the phase transitions of these heuristics are probably the only way to really compare one implementation from another one and bring clarity to this jungle. Beyond clarity, phase transitions provide a unique navigational tool ( see The Map Makers) to the users.
 
Notations
 
In terms of notations, A, L, S and N refers to a general, a low rank, a sparse and a noisy matrix respectively. This page lists the different codes that implement some of these matrix factorizations: Matrix Completion, Robust PCA , Noisy Robust PCA, Sparse PCA, NMF, Dictionary Learning, MMV, Randomized Algorithms and other factorizations. Some of these toolboxes can sometimes implement several of these decompositions and are listed accordingly in each decomposition/factorization. Before appearing on this page,  I generally feature these algorithms on Nuit Blanche under the MF tag: http://nuit-blanche.blogspot.com/search/label/MF . You can also subscribe to the Nuit Blanche feed,
 
Finally, you are also welcome to join the Advanced Matrix Factorization Group on LinkedIn or the Google+ community.
Randomized Algorithms ( Randomized Numerical Linear Algebra (RandNLA))


Phase Transitions:
  • None so far.
Implementations:
 
These algorithms uses random projections to shrink very large problems into smaller ones that can be amenable to traditional matrix factorization methods (see Streaming Data Mining Tutorial slides (and more) )
 
 
Kernel Factorizations, Positive Kernel K(x,x') = G(f(x)*f'(x'))
(Reproducing Hilbert Kernel Spaces, Variable separation, Multipole methods,...)
Phase Transitions:
  • None so far.
Implementations:
 
 
Spectral Clustering: A = DX  with unknown D and X, solve for sparse X and X_i = 0 or 1
 
 
 
K-Means / K-Median: A = DX  with unknown D and X, solve for XX^T = I and X_i = 0 or 1
 
Phase Transitions:
Implementations:
 
 
Subspace Clustering: A = AX  with unknown X, solve for sparse/other conditions on X  
 
From: Robust and Efficient Subspace Segmentation via Least Squares Regression by Canyi Lu, Hai Min, Zhong-Qiu Zhao, Lin Zhu, De-Shuang Huang, and Shuicheng Yan
From LSR 

by Canyi Lu, Hai Min, Zhong-Qiu Zhao, Lin Zhu, De-Shuang Huang, and Shuicheng Yan

Phase Transitions:
  • None so far.
Implementations:
 
Graph Matching: A = XBX^T with unknown X, B solve for X as a permutation
Phase Transitions:
Implementations:
  • None so far.

 
Non-Negative Matrix Factorization / NMF: A = DX with unknown D and X, 
solve for elements of D,X > 0
 

Phase Transitions:
  • None so far.
Implementations:

Non-Negative Tensor Factorizations
 
Phase Transitions:
  • None so far.
Implementations:
 
 
Generalized Matrix Factorization 
W.*L − W.*UV′ with W a known binary mask, U,V unknowns solve for U,V and L lowest rank possible
 
Phase Transitions:
  • None so far.
Implementations:
 
 
Matrix Completion, A = H.*L with H a known mask, L unknown solve for L lowest rank possible
 
Phase Transitions:
 


Implementations:
 

The idea of this approach is to complete the unknown coefficients of a matrix based on the fact that the matrix is known to be low rank in advance:

 
 
 

YouTube Video


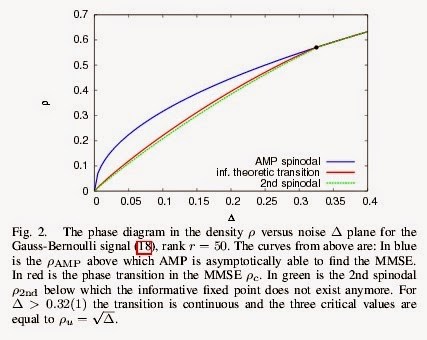
Stable Principle Component Pursuit (SPCP)/ Noisy Robust PCA,  A = L + S + N with L, S, N unknown, solve for L low rank, S sparse, N noise


Phase Transitions:
 
  • None so far
 
Implementations:
 
Robust PCA : A = L + S with L, S unknown, solve for L low rank, S sparse
Phase Transitions:
Implementations:


Sparse PCA: A = DX  with unknown D and X, solve for sparse D 


 
Sparse PCA on wikipedia
 
Implementations:
 
 
Dictionary Learning: A = DX  with unknown D and X, solve for sparse X 


Phase Transitions:
 


Implementations:
 
Some implementations of dictionary learning implement the NMF also
 
Archetypal Analysis: A = DX with unknown D and X, solve for D = AB with D, B positive

Phase Transitions:

 
Multiple Measurement Vector (MMV) Y = A X with unknown X and rows of X are sparse.
Phase Transitions:
 


 
Compressive Sensing/SMV, Y = A X with unknown X and rows of X are sparse, X is one column.
 
Compressive sensing is a special case of MMV called Single Measurement Vector (SMV)
 
Phase Transitions:
 

 


Blind Source Separation (BSS) Y = A X with unknown A and X and statistical independence between columns of X or subspaces of columns of X
Phase Transitions:
  • None so far.
Implementations:
 

Include Independent Component Analysis (ICA), Independent Subspace Analysis (ISA), and Sparse Component Analysis (SCA). There are many available codes for ICA and some for SCA. Here is a non-exhaustive list of some famous ones (which are not limited to linear instantaneous mixtures). TBC

ICA:


SCA:

 
Partial and Online SVD/PCA
 
Phase Transitions:
  • None so far.
Implementations:
 
Online SVD
Partial SVDs:

Other factorization
D(T(.)) = L + E with unknown L, E and unknown transformation T and  solve for transformation T, Low Rank L and Noise E
Phase Transitions:
  • None so far.
Implementations:


 
 
Boolean Matrix Factorization Tensor Decomposition
Phase Transitions:
  • None so far.
Implementations:


Tensor Decomposition


 
 
Frameworks featuring advanced Matrix factorizations


 
For the time being, few have integrated the most recent factorizations.
GraphLab / Hadoop
 
Books
 
 
 
Sources
Relevant links
 

Map

counter for tumblr
Tags :

留下你的评论